√100以上 p(x y) independent 102041-P(x y) independent

The events X and Y are said to be independent if the probability of X is not affected by the occurrence of Y That is, X, Y independent if and only if P(XY)=P(ot Y) Here P(XY) means theBut using the de nition of conditional probability we nd that P(Y = jX= ) = P(Y = \X= ) P(X= ) = P(Y = ) or P(Y = \X= ) = P(X= )P(Y = ) This formula is symmetric in Xand Y and so if Y is independent of Xthen Xis alsoIn real life, we usually need to deal with more than one random variable For example, if you study physical characteristics of people in a certain area, you might pick a person at random and then look at his/her weight, height, etc

Http Web Eecs Umich Edu Fessler Course 401 E 94 Fin Pdf

P(x y) independent

P(x y) independent-P(X) = P(Y) or P(X n Y) = 0 That is, the above is true if and only if X and Y are equally likely, or if X and Y are mutually exclusive Oh, and since we were dividing by P(X) and P(Y), both must be possible, ie nonzero probabilityDefine Z = max (X, Y), W = min (X, Y) Find the CDFs of Z and W Solution To find the CDF of Z, we can write F Z ( z) = P ( Z ≤ z) = P ( max ( X, Y) ≤ z) = P ( ( X ≤ z) and ( Y ≤ z)) = P ( X ≤ z) P ( Y ≤ z) ( since X and Y are independent) = F X ( z) F Y ( z)

Joint Cumulative Distributive Function Marginal Pmf Cdf

Sometimes it really is, but in general it is not Especially, Z is distributed uniformly on (1,1) and independent of the ratio Y/X, thus, P ( Z ≤ 05 Y/X) = 075 On the other hand, the inequality z ≤ 05 holds on an arc of the circle x 2 y 2 z 2 = 1, y = cx (for any given c) The length of the arc is 2/3 of the length of the circle2 Independent Random Variables The random variables X and Y are said to be independent if for any two sets of real numbers A and B, (24) P(X 2 A;Y 2 B) = P(X 2 A)P(Y 2 B) Loosely speaking, X and Y are independent if knowing the value of one of the random variables does not change the distribution of the other ran(d) YES, X and Y are independent, since fX(x)fY (y) = ˆ 2x·2y = 4xy if 0 ≤ x ≤ 1 and 0 ≤ y ≤ 1 0otherwise is exactly the same as f(x,y), the joint density, for all x and y Example 4 X and Y are independent continuous random variables, each with pdf g(w) = ˆ 2w if 0 ≤ w ≤ 1 0, otherwise (a) Find P(X Y ≤ 1) (b)

Since X X X and Y Y Y are independent, P (X = a i and Y = b j) = P (X = a i) ⋅ P (Y = b j) P(X = a_i \text{ and } Y = b_j) = P(X = a_i) \cdot P(Y = b_j) P (X = a i and Y = b j ) = P (X = a i ) ⋅ P (Y = b j ) and it follows that E X ⋅ Y = ∑ i, j P (X = a i) ⋅ P (Y = b j) a i b j = (∑ i P (X = a i) a i) (∑ j P (Y = b j) b j) = E X ⋅ E YRandom variables X and Y are independent if their joint distribution function factors into the product of their marginal distribution functions • Theorem Suppose X and Y are jointly continuous random variables X and Y are independent if and only if given any two densities for X and Y their product is the joint density for the pair (X,Y) ie ProofY y' to mean the event 'X x and Y y' The joint cumulative distribution function (joint cdf) is de ned as F(x;y) = P(X x;

TEDx was created in the spirit of TED's mission, "ideas worth spreading" It supports independent organizers who want to create a TEDlike event in their own communityFigure1 f(x;y)j0 < x < 1;0 < y < 1g Note that f(x;y) is a valid pdf because P (1 < X < 1;1 < Y < 1) = P (0 < X < 1;0 < Y < 1) = Z1 1 Z1 1 f(x;y)dxdy = 6 Z1 0 Z1 0 x2ydxdy = 6 Z1 0 y 8 < Z1 0 x2dx 9 =;The notation P(xy) means P(x) given event y has occurred, this notation is used in conditional probability There are two cases if x and y are dependent or if x and y are independent Case 1) P(xy) = P(x&y)/P(y) Case 2) P(xy) = P(x)

Worked Examples Multiple Random Variables Pdf Free Download

Answered Let X And Y Be Jointly Continuous Bartleby

We say that X and Y are independent if P (X = x, Y = y) = P (X = x) P (Y = y), for all x, y In general, if two random variables are independent, then you can write P (X ∈ A, Y ∈ B) = P (X ∈ A) P (Y ∈ B), for all sets A and BFigure1 f(x;y)j0 < x < 1;0 < y < 1g Note that f(x;y) is a valid pdf because P (1 < X < 1;1 < Y < 1) = P (0 < X < 1;0 < Y < 1) = Z1 1 Z1 1 f(x;y)dxdy = 6 Z1 0 Z1 0 x2ydxdy = 6 Z1 0 y 8 < Z1 0 x2dx 9 =;Y y) Continuous case If X and Y are continuous random variables with joint density f(x;y)

Please Show Work Will Upvote Rate 4 Expectation Of Product Of Random Variables Proof From The Definition Of The Ex Homeworklib

Http Homepage Stat Uiowa Edu Rdecook Stat Hw Hw7 Pdf

PXY=1(2) = p(2,1)/pY (1) = 01/06 = 1/6 2 If X and Y are independent Poisson RVs with respective meansY is independent of Xif P(Y = jX= ) = P(Y = ) for all ;Even if X and Y are independent, P(X ≤ x) P(Y ≤ y) ≠ P(X ≤ y) P(Y ≤ x) unless they are also identically distributed $\endgroup$ – farmer Jan 7 '19 at 2139 1

Pdf Probability And Statistics Test Set 6 Narender Palugula Academia Edu

Bayes Theorem Solutions Formulas Examples Videos

Answer Two events, X and Y, are independent if X occurs won't impact the probability of Y occurring More examples of independent events are when a coin lands on heads after a toss and when we roll a 5 on a single 6sided die Then, when selecting a marble from a jar and the coin lands on the head after a tossLet X and Y be two discrete variables whose joint pmf has the following values p(1, 1) = 1/4 , p(1, 0) = 1/2 , p(0, 1) = 1/12 , p(0, 0) = 1/6 and is 0 elsewhere Are X and Y independ Create anIf X and Y are independent, then E(es(XY )) = E(esXesY) = E(esX)E(esY), and we conclude that the mgf of an independent sum is the product of the individual mgf's Sometimes to stress the particular rv X, we write M X(s) Then the above independence property can be concisely expressed as M

Ece Umd Edu Sites Ece Umd Edu Files Resource Documents 19s Probability Pdf

2

P(y = \x= ) = p(x= )p(y = ) This formula is symmetric in Xand Y and so if Y is independent of Xthen Xis also independent of Y and we just say that Xand Y are independentDy = 6 Z1 0 y 3 dy = 1 Following the de–nition of the marginal distribution, we can get a marginal distribution for X For 0 < x < 1, f(x) ZNow assume Z independent of X given Y, and assume W independent of X and Y given Z, then we obtain P(X=x,Y=y,Z=z,W=w) = P(X=x)P(Y=yX=x)P(Z=zY=y)P(W=wZ=z) For binary variables the representation requires 1 2*1 2*1 2*1 = 1(41)*2 numbers significantly less!!

Problems And Solutions 4

Www Ocf Berkeley Edu Kedo Notes Cs 1 Mt2 Pdf

1 2 0 a 1 16 0 b 1 16 0 c 1 16 0 d 1 16 1 a 1 16 1 b 1 16 1 c 1 16Conditional independence Markov Models2 (MU 27) Let X and Y be independent geometric random variables, where X has parameter p and Y has parameter q (a) What is the probability that X = Y?

2

Get Answer Let X And Y Be Independent Binomial Random Variables Having Transtutors

Suppose X and Y are jointlydistributed random variables We will use the notation 'X x;Loosely speaking, X and Y are independent if knowing the value of one of the random variables does not change the distribution of the other random variable Random variables that are not independent are said to be dependent For discrete random variables, the condition of independence is equivalent to P(X = x;Y = y) = P(X = x)P(Y = y) for all x, yNote that without independence, the last conditional distribution stays as such (in the independent case, it would be equal to P Y

Www Stat Auckland Ac Nz Fewster 325 Notes Ch3annotated Pdf

Y 8 P X Y 7 P Xy 14 B Find The Corr X Y 5 For The Bivariate Negative Binomial Course Hero

X and Y are independent, if for any "good" subsets A, B, like finite or infinite intervals, P (X ∈ A, Y ∈ B) = P (X ∈ A) P (Y ∈ B) (2) Let us prove, first, that property 1 implies 2 By (1), we have P (X ∈ A, Y ∈ B) = Z A Z B f (x, y) dy dx = Z A Z B f X (x) f Y (y) dy dx = Z A f X (x) Z B f Y (y) dy dx = Z A f X (x) dx Z B f YWeek 9 1 Independence of random variables • Definition Random variables X and Y are independent if their joint distribution function factors into the product of their marginal distribution functions • Theorem Suppose X and Y are jointly continuous random variablesX and Y are independent if and only if given any two densities for X and Y their product is the joint density for the pair (X,YProblem Consider two random variables $X$ and $Y$ with joint PMF given in Table 53 Find $P(X \leq 2, Y \leq 4)$ Find the marginal PMFs of $X$ and $Y$

Joint Probability Definition

Faculty Math Illinois Edu Zvondra 461f14 Ts3 Pdf

Let X Exponential (px), And Y ^ Exponential (hy) Further Assume X And Y Are Independent (a) Compute P(X = Min (X,Y)) (b) Derive The Pdf For S = Min (X,Y) (c) Derive The Pdf For T = Max (X,Y) (d) Derive The Joint Pdf For S = Min (X,Y) And T = Max (X,Y) (e) Derive The Joint Pdf For U = 2 Min (X,Y) And V = Max(X,Y) Min (X,Y) (f) ComputeIf \(X\) and \(Y\) are independent, discrete random variables, then the following are true \begin{align*} p_{XY}(xy) &= p_X(x) \\ p_{YX}(yx) &= p_Y(y) \end{align*} In other words, if \(X\) and \(Y\) are independent, then knowing the value of one random variable does not affect the probability of the other oneThe notation P (xy) means P (x) given event y has occurred, this notation is used in conditional probability There are two cases if x and y are dependent or if x and y are independent Case 1) P (xy) = P (x&y)/P (y) Case 2) P (xy) = P (x) Share edited Feb 28 '17 at 2102 Yves Daoust

Help Prove X Y Are Conditionally Independent Given Z Iff b P X Z Y F X Z For Some Function F Mathematics Stack Exchange

Http Www Math Uiuc Edu Rsong 461f10 Whw10s Pdf

Dy = 6 Z1 0 y 3 dy = 1 Following the de–nition of the marginal distribution, we can get a marginal distribution for X For 0 < x < 1, f(x) ZThen, finding the probability that X is greater than Y reduces to a normal probability calculation P ( X > Y) = P ( X − Y > 0) = P ( Z > 0 − 55 ) = P ( Z > − 1 2) = P ( Z < 1 2) = That is, the probability that the first student's Math score is greater than the second student's Verbal score isX ~ b(n, p) is given by M(t, X) = (q pe^(t))^n Further, we know that for any two independent variates X, Y , the MGF of (XY)=M(t, XY) =M(t, X)xM(t, Y) = (q pe^(t))^n (q pe^(t))^m = (q pe^(t))^(nm) But this is clearly the MGF of a Binomial distribution with parameters (nm) and p ie b((nm), p)

Http Site Iugaza Edu Ps Masmar Files Problem Set 1 Pdf

Case Edu Artsci Math Mwmeckes Math3 s Hw01 13 Pdf

PX = Y = X x (1−p)x−1p(1−q)x−1q = X x (1−p)(1−q)x−1 pq Recall that from page 31, for geometric random variables, we have the identity PX ≥ i = X∞ n=i (1−p)n−1p = (1−p)i−1 (1)We can find the requested probability by noting that \(P(X>Y)=P(XY>0)\), and then taking advantage of what we know about the distribution of \(XY\) That is, \(XY\) is normally distributed with a mean of 55 and variance of as the following calculation illustrates• Let X and Y be independent random variables X ~ Bin(n 1, p) and Y ~ Bin(n 2, p) X Y ~ Bin(n 1 n 2, p) • Intuition X has n 1 trials and Y has n 2 trials o Each trial has same "success" probability p Define Z to be n 1 n 2 trials, each with success prob p Z ~ Bin(n 1 n 2, p), and also Z = X Y • More generally X i ~ Bin(n i

The Random Variable X And Y Have The Following Joint Probability Mass Function P X Y 23 0 2 Homeworklib

Www Stat Auckland Ac Nz Fewster 325 Notes Ch3annotated Pdf

Two random variables X and Y are independent iff for all x, y P(X=x, Y=y) = P(X=x) P(Y=y) Representing a probability distribution over a set of random variables X 1, XPX(x), satisfythe conditions a pX(x) ≥ 0 for each value within its domain b P x pX(x)=1,where the summationextends over all the values within itsdomain 15 Examples of probability mass functions 151 Example 1 Find a formula for the probability distribution of the total number of heads obtained in four tossesof a balanced coinTheorem If X and Y are independent events, then the events X and Y' are also independent Proof The events A and B are independent, so, P(X ∩ Y) = P(X) P(Y) Let us draw a Venn diagram for this condition From the Venn diagram, we see that the events X ∩ Y and X ∩ Y' are mutually exclusive and together they form the event X

Independent Versus Dependent Pdf Physics Forums

Ocw Mit Edu Resources Res 6 012 Introduction To Probability Spring 18 Part I The Fundamentals Mitres 6 012s18 L12as Pdf

X and Y are independent if and only if p(x,y) = p X(x)p Y (y) for all (x,y) ∈ R2 Proof First suppose X and Y are independent Then for any (x,y) ∈ R, p(x,y) = P(X = x,Y = y) = P(X = x)P(Y = y) = p X(x)p Y (y) Now suppose p(x,y) = p X(x)p Y (y) for all (x,y) ∈ R Then for any A ⊂ R and B ⊂ R we have P(X ∈ A,Y ∈ B) = X x∈A X y∈B P(X = x,Y = y) = X x∈A X y∈B p X(x)p Y (y) 1 =P (X) = P (Y) or P (X n Y) = 0 That is, the above is true if and only if X and Y are equally likely, or if X and Y are mutually exclusive Oh, and since we were dividing by P (X) and P (Y), bothAccording to the definition, X and Y are independent if p (x, y) = p X (x) ⋅ p Y (y), for all pairs (x, y) Recall that the joint pmf for (X, Y) is given in Table 1 and that the marginal pmf's for X and Y are given in Table 2

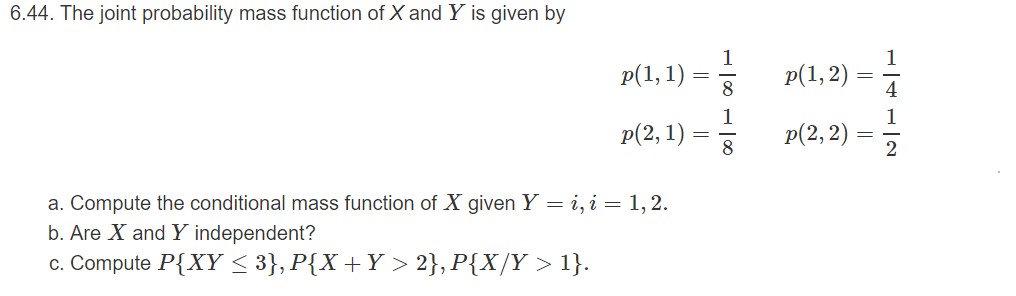
Answered 6 44 The Joint Probability Mass Bartleby

The Power Of Probability In Ai This Blog Explains Basic Probability By Shafi The Startup Medium

Note that if X and Y are independent, we have p XY(x;y) = p X(x) p Y(y), so the log term is log 2 1 = 0, which implies that we can't save any bits in generating XY 5 Example 51 Consider the following joint distribution x y p XY(x;y)?Independent Events Venn Diagram Let us proof the condition of independent events using a Venn diagram Theorem If X and Y are independent events, then the events X and Y' are also independent Proof The events A and B are independent, so, P(X ∩ Y) = P(X) P(Y) Let us draw a Venn diagram for this conditionP(X = 1 ∩ Y = 1) = p (1, 1) = 010 = 025 × 040 = P(X = 1) × P(Y = 1) {X = 1} independentand {Y = 1} are Def independentRandom variables X and Y are if and only if discrete p (x, y) = p X (x) ⋅ p Y (y) for all x, y continuous f (x, y) = f X (x) ⋅ f Y (y) for all x, y F (x, y) = P (X

Math Hmc Edu Benjamin Wp Content Uploads Sites 5 19 06 The Long And Short Of Benford E2 80 99s Law Pdf

Isagani Briones Information Theory Assign 1 Studocu

If we think of W 1 as the number of trials we have to make to get the first success, and then W 2 the number of further trials to the second success, and so on, we can see that X = W 1 W 2 W r, and that the W i are independent and geometric random variables So EX = r/p, and Var(X) = r(1−p)/p2 5 Poisson random variablesNote that without independence, the last conditional distribution stays as such (in the independent case, it would be equal to P YThe random variables \(X\) and \(Y\) are independent if and only if \(P(X=x, Y=y)=P(X=x)\times P(Y=y)\) for all \(x\in S_1, y\in S_2\) Otherwise, \(X\) and \(Y\) are said to be dependent Now, suppose we were given a joint probability mass function \(f(x, y)\), and we wanted to find the mean of \(X\) Well, one strategy would be to find the

2

Two Independent Random Variables X And Y Are Uniformly Distributed In The Interval 1 1 Gate 12 Youtube

Cov(X;Y) p V(X)V(Y) = ˙XY ˙X˙Y Notice that the numerator is the covariance, but it's now been scaled according to the standard deviation of Xand Y (which are both >0), we're just scaling the covariance NOTE Covariance and correlation will have the same sign (positive or negative) 14Example \(\PageIndex{1}\) For an example of conditional distributions for discrete random variables, we return to the context of Example 511, where the underlying probability experiment was to flip a fair coin three times, and the random variable \(X\) denoted the number of heads obtained and the random variable \(Y\) denoted the winnings when betting on the placement of the first headsThe weight of each bottle (Y) and the volume of laundry detergent it contains (X) are measured Marginal probability distribution If more than one random variable is defined in a random experiment, it is important to distinguish between the joint probability distribution of X and Y and the probability distribution of each variable individually

Independent Variables And Chi Square Independent Versus Dependent Variables Given Two Variables X And Y They Are Said To Be Independent If The Occurance Ppt Download

Solved A Are X And Y Independent Explain B Are X Chegg Com

A) Are events {X = 1} and {Y = 1} independent?

Processing Math 100 Home Table Of Contents Conditional Distribution Unconditionals In Terms Of Conditionals More Than 2 Variables Substitution Problems For Practice Conditional Distribution Definition Conditional Distribution Let X W S And Y W T Be

Stats Cheat Sheet Coefficient Of Variation Variance

Chapter 3 Conditional Probability Problems If And Are Both Discrete Show That For All Such That Py In My Own Words The Question Asks Whether The Sum Of For Studeersnel

Http Www Inf Ed Ac Uk Teaching Courses Iaml Slides Naive 2x2 Pdf

Journal Of Statistics Education V13n3 Sheldon Stein

Joint Cumulative Distributive Function Marginal Pmf Cdf

2

Http Projecteuclid Org Download Pdf 1 Euclid Aop

Problems And Solutions 4

2

Arxiv Org Pdf 1903

Http Www Cl Cam Ac Uk Teaching 1314 Infotheory Exercises1to4 Pdf

Http Athenasc Com Bivariate Normal Pdf

2

Worked Examples Multiple Random Variables Pdf Free Download

Conditional Independence As With Absolute Independence The Equivalent Forms Of X And Y Being Conditionally Independent Given Z Can Also Be Used P X Y Ppt Download

Http Math Iisc Ac In Manju Pt19 Hwk 2 19 Pdf

2

Http Web Eecs Umich Edu Fessler Course 401 E 94 Fin Pdf

Www Math Utah Edu Davar Math5010 S07 Finprac Finprac Pdf

A P Overline X Cap Y Frac 1 2 X And Y Are Not Independent B X And Y Are Independen D P X Cup Y Frac 2 2 401

Suppose That X Binomial N P And Y Binomial M P Suppose Also That X And Y Are Independent What Is The Distribution Of X Y Quora

Why Is Naive Bayes Theorem So Naive By Chayan Kathuria The Startup Medium

Solved 4 Suppose That X And Y Are Independent Exp 1 Ran Chegg Com

Need Your Help In Probability Problems Thanks Socratic

2

Consider Two Independent Random Variables X And Y With Identical Distributions Gate Ec 09 Youtube

Courses Edx Org C4x Mitx 6 041x 1 Asset Resources Exam3 Pdf

Http Www Cs Cmu Edu rti Class Slides Nbayes 9 22 11 Pdf

Conf Math Illinois Edu Rsong 461f10 Whw10 Pdf

Product Distribution Wikipedia

Naive Bayes Summary Programmer Sought

Cdn Prexams Com 1814 Kobeissi Final Spring07 08 Pdf

Solved Exercise2 Consider Two Independent Random Variable Chegg Com

2

Two Events X And Y Are Independent Of Each Other P Y 5 6 An

Ppt Probability Statistics Lecture 8 Powerpoint Presentation Free Download Id

Solved Let X Geom P And Y Bern 1 P Be Independent S Chegg Com

Processing Math 100 Home Table Of Contents Standard Discrete Distributions Finite Sample Space Discrete Uniform Bernoulli Binomial Hypergeometric Relation Between Binomial And Hypergeometric Problems For Practice Standard Discrete Distributions

Solved Problems Pdf Jointly Continuous Random Variables

2

Q Tbn And9gctzicckryrhmi12kq9tar6cbpxap5yyg5peziwbeky9x Pofvnm Usqp Cau

Assignment On Random Variables

The Joint Probability Mass Function Of X And Y Is Given By Px Y 1 1 Px Y 1 2 3 Px Y 1 3 00 1 Px Y 2 1 Px Y 2 2 3 Course Hero

When A Fact Becomes Evidence Letters To Nature

Http Cis Jhu Edu Bruno S05 310 Donexam2 Pdf

Ocw Mit Edu Resources Res 6 012 Introduction To Probability Spring 18 Part I The Fundamentals Mitres 6 012s18 L12as Pdf

Let X And Y Have Joint Density Xy 0otherwise 0 Otherwise A Find K B Compute The Homeworklib

Mkt 300 Lecture Notes Spring 18 Lecture 26 Chi Squared Test Conditional Probability Bayes Estimator

2

Http Www Math Cmu Edu Users Weikang Math325 Solhw8 Pdf

Hannig Cloudapps Unc Edu Stor435 Homeworks Hw08 Pdf

Http Isa Site Nthu Edu Tw App Index Php Action Downloadfile File Wvhsmflxtm9mekkytdncmflwohppre0wtvy4mu5urxdnrekwwhpjnu56ttnmbkjrwmc9pq Fname 0054rob0rksscd11ggxsnkxtdctwcglkwsfggcnk41jdoocckp30cdsw3454swuslowwttihdgpoegch34kob4npfgmojdhcccvxxwfc34b4wxklooporpfcss40ssxt

Product Distribution Wikipedia

Variance Of Sum And Difference Of Random Variables Video Khan Academy

2

2

Two Random Variables X Y Are X Y Independant B Are X Y X Y Independant Mathematics Stack Exchange

Http Sites Science Oregonstate Edu Deleenhp Teaching Fall16 Mth361 Lect Notes Chap6 Pdf

Http People Math Gatech Edu Mdamron6 Teaching Fall 15 Homework Math 6241 Hw 4 Pdf

2

Math 411 Homework 4

2

Http Www Eclecticon Info Index Htm Files Probability statistics expectation variance skew kurtosis Pdf

Solved Let X Y And Z Be Independent Uniform 0 1 Random Chegg Com

2

Http Web Tecnico Ulisboa Pt Andreas Wichert 21 Bn Pdf

Sheet 8 Probability Studocu

Gaussian Random Variable St Program Analysis And Mechanization Cs 591 Docsity

Q Tbn And9gcr25tef6v4nurws2kngeqzdif04iob3esypvergphtjedi 3mll Usqp Cau

Incoming Term: p(x y) independent,